Les emprunts indivis : Synthèse, exercice et test de connaissances

Pour acquérir un bien immobilier (ou un véhicule, une cave, un parking…), un particulier doit, s’il ne dispose pas des fonds suffisants, emprunter une somme d’argent auprès d’une banque. Cet emprunt va être contracté par le particulier et tenir compte des conditions de taux, de frais de dossier et d’assurance.

Tableau d’amortissement d’un emprunt indivis

Le tableau d’amortissement d’un emprunt indivis se présente sous la forme suivante :

La première annuité est toujours payée une période après avoir contracté l’emprunt (en général un an après), sauf indication contraire.

Modes de remboursement d’un emprunt

Un emprunt peut être remboursé selon l’une ou l’autre des modalités suivantes :

– remboursements par amortissements constants (la même fraction du capital fait l’objet d’un remboursement chaque année) ;
– remboursement « in fine » (le capital est remboursé en totalité à la fin de l’emprunt) ;
– remboursement par annuités constantes (cas le plus fréquent) :

1. Le particulier va payer la même somme chaque année, comprenant les intérêts et les amortissements, ce que l’on nomme « l’annuité ».
2. Annuités constantes avec différé de paiement (pas d’intérêts payés pendant le différé). Dans la pratique, le banquier parle de « crédit relais ». Le client ne va pas payer d’intérêt pendant une certaine période. En réalité, le montant de l’emprunt de départ est capitalisé (noté « dette » dans le tableau).

Capital restant dû

Le capital restant dû correspond à la somme à rembourser chaque année. Le capital restant dû la dixième année signifie qu’il s’agit du capital restant dû après le paiement de la 9e annuité. Il s’obtient en faisant la différence entre le capital restant dû de départ et le montant des amortissements.

CRDU 1 = montant emprunté au départ

CRDU 2 = CRDU1 – amortissement de la première année…etc.

Intérêts

Le montant des intérêts correspond à la somme des intérêts à la charge de l’emprunteur.

Intérêts = Capital * Taux d’intérêt

Amortissement

L’amortissement correspond à la part de l’emprunt qui fait l’objet d’un remboursement.

Annuité

L’annuité correspond à la somme à payer par l’emprunteur chaque année. L’annuité est égale à la somme des intérêts et des amortissements.

REMARQUE IMPORTANTE : Le dernier amortissement de l’emprunt est égal au capital restant dû au titre de la dernière année. Le capital restant dû à une date quelconque est égal à la valeur actuelle des annuités qui restent à payer. Dans le cadre d’un emprunt indivis à annuités constantes, les amortissements sont en progression géométrique de raison q = (1 + i). Ici, i correspond au taux d’intérêt.

Taux effectif global (TEG)

Le taux effectif global doit tenir compte du taux, des frais d’assurance et des frais de dossier. Il s’agit de calculer le coût réel de l’emprunt et donc le taux réel de l’emprunt.

Pour calculer le taux effectif global, il faut retirer du montant de l’emprunt les frais de dossier et l’égaliser avec les annuités actualisées correspondantes. En réalité, il faudra majorer l’annuité du montant de la prime d’assurance correspondante (si la prime calculée est du même montant et que les versements sont constants). Il est possible de retrouver ce taux en utilisant une interpolation linéaire .

Le cas le plus complexe en matière d’emprunt indivis concerne les remboursements avec annuités constantes et différés de paiement (aucun intérêt n’est payé pendant le différé).

EXEMPLE : 5 annuités avec 2 ans de différé ; t = 6 % ; Emprunt = 200 000 €

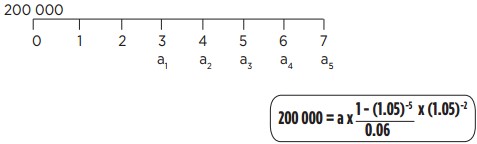
Annuités constantes = 53 347.72 €

Les deux premières années, il n’y aura ni intérêts, ni amortissements, ni annuités de paiements dans le tableau. Une colonne supplémentaire va être ajoutée, appelée « dette ». Les 2 premières années, on multiplie le capital par (1+i) pour obtenir le montant de la dette. à l’issue de la première annuité, donc de la troisième année, on effectue les calculs suivants :

Il est logique que le montant du capital soit majoré des intérêts puisque l’emprunteur ne va rien payer pendant ces deux ans de différé. Ceci va venir augmenter le montant de la dette. Ensuite, l’emprunteur va commencer à rembourser son emprunt en payant sa première annuité. Donc, le montant de la dette va diminuer à partir du paiement de la première annuité. Le tableau ci-dessous est identique à un tableau d’amortissement indivis mais il est complété par la colonne « Dette ».

Tableau d’emprunt indivis avec annuités constantes et différé d’une année

Les emprunts indivis : Exercices d’entraînement

Les emprunts indivis : Télécharger la correction des exercices

Télécharger “Emprunt indivis” Téléchargé 173 fois – 6 Mo