Après avoir établi le programme des ventes, il est nécessaire d’adapter le programme de production à la demande prévisionnelle et d’effectuer les ajustements nécessaires. La gestion budgétaire de la production comprend trois étapes :
- la détermination du programme optimal de production à l’aide d’outils mathématiques ou informatiques ;
- l’élaboration du budget de production, en terme de moyens, conforme au programme de production et valorisé par les coûts préétablis des produits ;
- le contrôle budgétaire de la production effectué à partir de l’analyse des écarts entre les réalisations et les prévisions.
Le programme de production
Une organisation performante de la gestion de la production doit répondre à plusieurs objectifs :
– maîtriser les flux des matières,des composants,entrant dans le processus de production et des produits ;
– optimiser les capacités de production;
– organiser le travail selon les choix stratégiques adoptés(intégration,sous-traitance,externalisation…);
– améliorer la qualité des produits;
– minimiser les coûts;
– réduire les délais (approvisionnements, production,stockage…);
–satisfaire la clientèle, en adaptant rapidement les capacités de production à l’évolution de la demande.
En conséquence, l’entreprise doit rechercher, en univers certain, le meilleur programme de production possible, c’est-à-dire celui qui permet :
- de satisfaire la demande tant en quantité, qu’en qualité et en temps ;
- d’ utiliser pleinement les capacités de production (équipement, main-d’œuvre…) sous certaines contraintes (commerciales, techniques et humaines) ;
- d’ optimiser le résultat.
Pour déterminer ce programme de production optimal, l’entreprise utilise plusieurs outils mathématiques et informatiques, dont la gestion de la production assistée par ordinateur (GPAO).
La programmation linéaire
a) Définition
La programmation linéaire est une technique qui permet d’estimer le programme de production optimal.
Un programme linéaire est composé :
– de variables positives ou nulles qui sont les inconnues (le nombre de produits à fabriquer par exemple) ;
– d’une fonction économique à optimiser représentée par une équation correspondant soit à un résultat à maximiser (la marge sur coût variable par exemple) soit à un coût à minimiser ;
– de contraintes traduites par des inéquations linéaires qui expriment :
- le nombre de produits maximal ou minimal à fabriquer ou à vendre ;
- la consommation de facteurs rares de production (matière, heure machine…) des variables en tenant compte des limitations.
Le programme linéaire est présenté sous forme canonique.
La résolution du programme linéaire consiste à calculer la valeur des variables qui optimise la fonction économique.
b) La résolution graphique
Le programme linéaire peut être représenté graphiquement lorsqu’il n’existe que deux variables.
Le graphique permet de visualiser :
-chaque contrainte correspondant à un demi-plan délimité par une droite;
– la zone d’acceptabilité des contraintes représentée par un polygone ;
-le point optimum qui se situe à l‘intersection de deux droites ou sur un des sommets du polygone.
Exemple:
Une entreprise fabrique 2 produits T et U dont la marge sur coût variable unitaire est respectivement de 240 et de 350 . Les éléments suivants sont fournis, sachant que l’objectif recherché est de maximiser (MAX) la marge sur coût variable (MCV) :
Présentation du problème
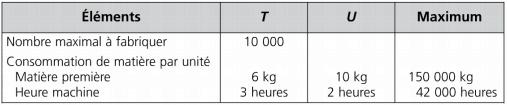
Variables :
x = quantité de T à fabriquer
y = quantité de U à fabriquer
Fonction économique :
[240 T + 350 U] = MAX MCV
Contraintes :
x ≥ 0
y ≥ 0
x ≤10 000 → contrainte commerciale
6x + 10y ≤ 150 000 → contrainte de production : matière
3x + 2y ≤ 42 000 → contrainte de production : heure machine
Représentation graphique
Droites :
D1, : x = 10 000 ; D2 : x = 6x + 10y = 150 000 ; D3 : 3x + 2y = 42 000
Graphique :
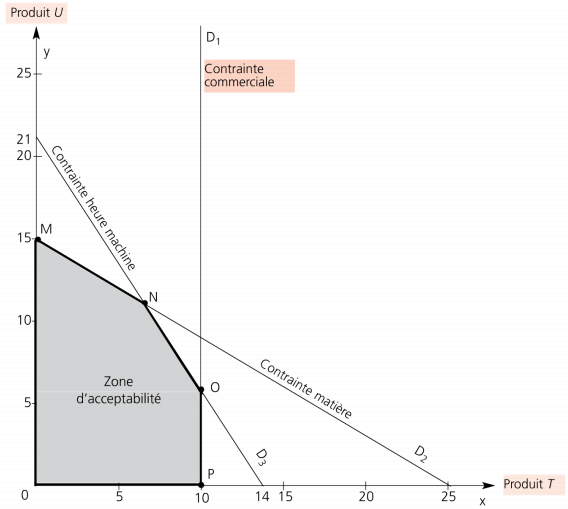
Le point N situé à l’intersection des droites des deux contraintes de production correspond à la saturation de ces contraintes pour x ≈ 6 667 et y = 11 000.
Recherche de l’optimum :
Il suffit de calculer la valeur de la fonction économique pour les points correspondant aux différents sommets :
– pour le point M : (240 x 0)+(350 x 15 000) = 5 250 000
– pour le point N : (240 x 6 667) + (350 x 11 000) = 5 450 080
– pour le point O : (240 x 10 000) + (350 x 6 000) = 4 500 000
La marge sur coût variable la plus élevée s’obtient au point N. Le programme optimum correspond à la production de 6 667 produits T et de 11 000 produits U.
Vérification de la saturation des contraintes : Contrainte de production matière : (6 x 6 667) + (10 x 11 000) = 150 000 (saturation)
Contrainte de production heure machine : (3 x 6 667) + (2 x 11 000) = 42 000 (saturation)
c) La résolution par la méthode du simplexe
La méthode du simplexe s’applique quel que soit le nombre des variables. La résolution du programme linéaire s’opère en trois étapes principales :
Transformer : les inéquations de contraintes en équations, en introduisant dans chacune d’elles une variable d’écart (e), de coefficient 1, qui représente une capacité commerciale ou de production inemployée.
Présenter : dans un tableau la solution de base par laquelle les variables (x et y) sont égales à 0 et les variables d’écart égales à la valeur de saturation de la contrainte.
Améliorer : progressivement la solution de base par une suite d’itérations pour aboutir à la solution optimale. La démarche est la suivante :
- entrer dans la solution la variable (x ou y) dont le coefficient est le plus élevé dans la fonction économique ;
- sortir de la solution la variable d’écart (e) dont le rapport : (Valeur de la contrainte / Coefficient) — est le plus faible sans être négatif ;
- calculer la valeur de la nouvelle solution (détail du calcul présenté dans l’application).
Exemple:
Le programme linéaire des deux produits T et U est le suivant :
Contraintes :
x ≥ 0
y ≥ 0
x ≤10 000
6x + 10y ≤ 150 000
3x + 2y ≤ 42 000
fonction économique :
[240 T + 350 U] = MAX MCV
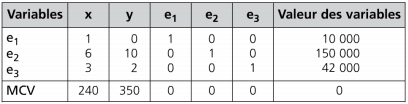
Équations avec variable d‘écart
x + e1 = 10 000
6x + 10y + e2 = 150 000
3x + 2y+ e3 = 42 000
[240 T + 350 U] = MAX MCV
Tableau relatif à la solution de base:
Première itération:
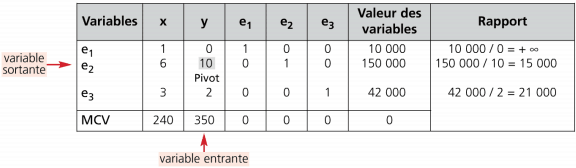 y se substitue à e2 ; les coefficients de la colonne e2 doivent donc apparaître dans la colonne y.
y se substitue à e2 ; les coefficients de la colonne e2 doivent donc apparaître dans la colonne y.
Tous les coefficients apparaissant sur la ligne du pivot doivent être divisés par ce dernier. On obtient :
0,6 ; 1 ; 0 ; 0,1 ; 0 ; 15 000
On constate qu’un 1 apparaît à la place du pivot. Il faut faire figurer un 0 dans les autres lignes de la colonne du pivot :
– ligne e3 : pour obtenir 0 à la place de 2, on retranche à la ligne e3 (e2 / 10) 2
-ligne MCV : pour obtenir 0 à la place de 350,on retranche à la ligne MCV (e2 / 10) 350
On obtient le nouveau tableau suivant :
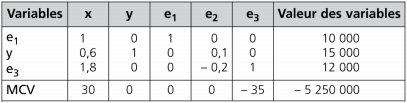 La solution est : x = 0 ; y = 15 000 ; en = 10 000 ; e3 = 12 000
La solution est : x = 0 ; y = 15 000 ; en = 10 000 ; e3 = 12 000
Cette solution est améliorable puisque la ligne MCV comporte une valeur positive.
Deuxième itération:
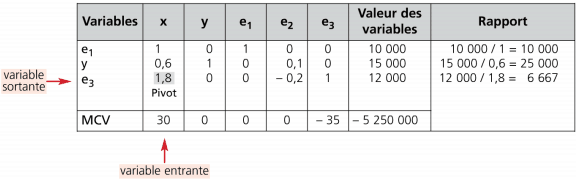 x se substitue à e3 ; les coefficients de la colonne e3 doivent donc apparaître dans la colonne x .
x se substitue à e3 ; les coefficients de la colonne e3 doivent donc apparaître dans la colonne x .
En appliquant les règles de calcul identiques à celles présentées pour la première itération, on aboutit au tableau ci-dessous :
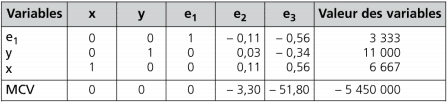
La ligne MCV ne comporte que des valeurs négatives, la solution optimale est donc atteinte. La solution optimale est : x = 6 667 produits T ; y = 11 000 produits U , e1 = 3 333 car la contrainte commerciale est de 10 000 produits 7 (10 000 – 6 667= 3 333)
MCV = (240 x 6 667) + (350 x 11 000) ≈ 5 450 000
Une résolution informatique, plus simple et plus rapide, est possible grâce à l’utilisation d’un module spécifique intégré dans les logiciels tableurs.
Le programme des composants
a) Principe
Une fois le programme de fabrication établi, à partir des prévisions de ventes, il faut planifier les besoins (quantités, délais de disponibilité) en composants (ensembles, sous-ensembles, pièces, matières premières) pour fabriquer les produits afin de gérer au mieux les stocks et les flux de composants nécessaires.
L’entreprise élabore à cet effet des documents tels que : les nomenclatures et les gammes de fabrication qui fournissent l’ensemble des informations techniques sur la fabrication d’un produit (la nature, le code, la quantité des composants utilisés aux différents stades de la production avec les temps de fabrication…).
b) Le calcul des besoins en composants
Le calcul des besoins en composants, en fonction des ventes futures et sur la durée du processus de production, peut s’effectuer à partir des nomenclatures par une suite de multiplications de matrices.
Par exemple, le calcul des besoins en ensembles E1, E2 dont le délai d’assemblage est de 2 mois, pour 2 produits X, Y en fonction des ventes prévisionnelles du premier trimestre est le suivant :
– matrice nombre d’ensembles par produit : MPe
– matrice commandes prévisionnelles (en milliers) : MCp
– Besoins en ensembles = (MPe) x (MCp)
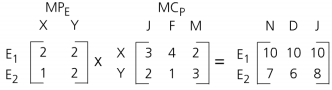
Pour les commandes de janvier, les ensembles et E2 doivent être disponibles en novembre à raison de :
(2 E1 x 3X) + (2 E1 x 2 Y) = 10 E1
(1 E2 x 3 X) + (2 E2 x 2 Y) = 7 E2
Le raisonnement est identique pour les commandes de février et mars.
Des progiciels MRP (management des ressources productives) sont utilisés par les entreprises pour gérer, avec précision, la fabrication prévisionnelle de produits nécessitant plusieurs niveaux de nomenclatures ainsi que de nombreux composants dont les stocks dépendent les uns des autres.
c) La gestion des goulots d’étranglement
Un goulot d’étranglement apparaît lorsque l’entreprise constate un manque de capacités productives ou des facteurs rares de production (approvisionnement, temps d’utilisation des postes de travail…) pour faire face aux besoins de production.
L’évaluation du manque de capacité s’effectue par différence entre les capacités nécessaires et les capacités disponibles pour chaque produit et pour chaque étape ou poste de travail du processus de fabrication.
Le goulot d’étranglement doit être géré de façon optimale, ce qui consiste pour l’entreprise à établir le programme de production en privilégiant la production du produit qui dégage une marge sur coût variable par unité de goulot d’étranglement supérieure aux autres produits.
Marge sur coût variable par unité de goulot d’étranglement = Marge sur coût variable par produit/Nombre d’unités de goulot d’étranglement par produit
Le programme des ventes sera ajusté en conséquence.
L’ordonnancement des tâches de production
La gestion de la production consiste également à établir des calendriers (dates, durées) pour ordonner l’ensemble des tâches d’un projet de fabrication et déterminer la durée totale de sa réalisation.
Les techniques d’ordonnancement ont pour objectif :
- de minimiser les durées ;
- d’assurer le plein emploi des moyens ;
- de minimiser les coûts.
La gestion des stocks de produits
L’organisation de la production peut être gérée :
–en flux tendus : absence de stocks,d’après la méthode juste à temps (JAT) ou Kanban;
-en présence de stocks qui permettent de réguler les flux tout au long du processus de production et de satisfaire la demande ;
– avec une combinaison des deux en fonction des activités.
La gestion des stocks entraîne des coûts tels que :
– le coût de lancement de la fabrication des lots;
-le coût de stockage.
L’objectif de l’entreprise est de minimiser ces coûts tout en détenant en stock les quantités suffisantes pour faire face à la demande.
Le contrôle de la qualité
Le contrôle de la qualité est devenu un élément essentiel de la gestion de la production ; il doit s’effectuer tout au long du processus de production.
L’entreprise doit avoir comme objectif zéro défaut afin d’améliorer le produit, de minimiser ses coûts, de générer de la valeur et de satisfaire au maximum sa clientèle.
Il existe plusieurs outils et méthodes pour gérer la qualité (méthodes statistiques, diagramme de Pareto, diagramme cause-effet).
La budgétisation de la production
La budgétisation de la production permet aux différents responsables de la fonction de production de chiffrer le programme de production et de le ventiler en plusieurs budgets selon les besoins de l’entreprise.
Les différents budgets de production peuvent être consolidés et soumis à la direction générale pour approbation conjointement au budget général des ventes afin d’en vérifier la cohérence.
Le chiffrage des budgets de production s’effectue en coûts standards ou en coûts préétablis de production ; soit d’après la méthode classique des coûts complets, soit d’après la méthode des coûts à base d’activités, en distinguant :
- les charges directes de production (matières,main-d’œuvre);ce qui permet de connaître pour chaque ventilation les matières à consommer et le coût budgété de la main-d’œuvre directe ;
- les charges indirectes de production comprenant des charges variables ou fixes (budgets flexibles) ; ce qui permet de connaître pour chaque ventilation les charges indirectes de production.
La détermination des coûts préétablis a été étudiée dans un article précédent.
Le contrôle budgétaire
Le contrôle budgétaire de la production consiste à confronter :
- les coûts constatés pour la production réelle, provenant de la comptabilité de gestion (coût de production par produit, par activité, stocks de produits…) ;
- aux prévisions issues des budgets.
Le contrôle budgétaire de la production peut être mené de la manière suivante :
Analyser les écarts sur coûts préétablis significatifs :
Écarts sur charges directes : matières, composants, main-d’œuvre. On distingue trois niveaux d’analyse étudiés ;
Écarts sur charges indirectes: centres d’analyse. On distingue trois niveaux d’analyse étudiés.
Communiquer l’analyse des écarts: aux responsables concernés, pour que chacun apprécie les conséquences de ces écarts sur les activités qui lui sont confiées. Par exemple : un écart sur temps défavorable dans un atelier pose un problème de rendement. aux dirigeants afin qu’ils en tiennent compte au niveau de la stratégie globale de l’entreprise.
Porter un jugement éclairé : en fonction de la cause de l’écart. Par exemple : former le personnel ou embaucher du personnel qualifié de façon à augmenter la productivité.
Laisser un commentaire